Fingerprints and LeetCode Problem 1377

In last weekend's LeetCode Contest, there was an interesting problem that involved finding the fingerprint in a graph. It reminds me of some articles I've read on the topic, so I decided to write up my thoughts and share the solution to the coding challenge.

What Are Fingerprints?

Fingerprinting is a technique that is used in graph analysis to trace out paths in a network. I encountered this around Personalized PageRank computation techniques. In this scenario, you have a large graph, possibly millions of nodes, and you are interested in the neighborhood of nodes around a query node. Taking a Monte Carlo approach, you can drop a bunch of random walkers (particles) onto the query node and allow them to explore different paths by stepping from one node to the next across the graph edges. Each path that a walker takes is referred to as a fingerprint. The length of the fingerprint will depend on parameters set in the algorithm. In the end, all of the fingerprints can be combined to form a probability distribution over the nodes in the neighborhood of the query node. In the work Fogaras 2004, the authors show how the personalized pagerank of a node can be approximated from the final vertex of thousands of fingerprints. The resulting Personalized PageRank gives a good measure of the items within the neighborhood of interest of a target user and can be used to offer personalized recommendations.

I suspect that the terminology "fingerprint" is borrowed from molecular biology, where fingerprinting is a common strategy used to encode the structure of molecule. The challenge is to formulate a numerical representation of the structure of a molecule that can be used as a similarity measure when comparing molecules. It can also be used as the input to machine learning models. The basic idea is start at one atom in the molecule and make variable-length walks across the bonds until you have traced every substructure within the molecule. Doing this for each atom and combining the results give you a molecular fingerprint that can be easily compared to other molecules.

Chemical Similarity - Wikipedia

Solution to LeetCode Problem 1377

Every weekend, LeetCode holds a contest where partipants compete globally to solve four newly published coding challenges in 90minutes. The problems generally consist of an easy problem, two medium problems, and one hard problem in terms of difficulty. In the latest contest (Weekly Contest 179), the most difficult problem was a graph analysis challenge where, essentially, you are asked to find the fingerprint. The problem is linked and reproduced below.

Problem 1377. Frog Position After T Seconds

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex.

The edges of the undirected tree are given in the array edges, where edges[i] = [from i, to i] means there exists an edge connecting directly the vertices from i and to i.

Return the probability that after t seconds the frog is on the vertex target.

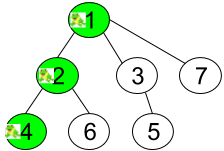
In the example above, the frog starts at node 1 and makes two hops to land on node 4 with a probability of 0.16.

Below I have posted my solution to the problem. The basic idea is to create a graph structure from the edges that are provided as input. Once you have a graph, a recursive depth-first search can be performed until the target node is reached. The tricky part involves tracking the probabilities and time steps during the recursion. Also, there are a few edge cases that need to be handled. In the end, this is very similar to the procedure laid forth in Fogaras 2004 to find the probability of landing on a final vertex using fingerprints.

class Solution {
public:

    using Edges = vector<vector<int>>; // list of edge pairs
    using Graph = map<int, vector<int>>; // adjacency lists

    Graph buildGraph(Edges & edges) {
        // build the adjacency lists
        Graph g;
        for (auto e : edges) {
            // theres no guarantee on the order of the edges
            // so add both directions for an undirected edge
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        return g;
    }

    double dfs(Graph & g, set<int> & marked, int node, int t, int target, double prob) {

        int count = 0;
        float max_prob = 0;

        // count how many nodes we can visit from here
        // but don't count the node we just jumped from
        for (auto nbor : g[node]) {
            if (!marked.count(nbor)) count++;
        }

        // check to see if we landed on the target
        if (node == target) {
            // landed here just in time
            if (t==0) return prob;

            // landed with time to spare, but no where to go
            else if (t>0 && count==0) return prob;

            // landed with time to spare, but other nodes to visit
            else if (t>0 && count) return 0;

            // did not make it in time (t<0)
            else return 0;
        }

        // continue the dfs recursion to other nbors
        for (auto nbor : g[node]) {
            if (marked.count(nbor)) continue;
            marked.insert(nbor);

            // go to next node
            // update the time to be less one step
            // update the probability to account for number of nodes
            float p = dfs(g, marked, nbor, t-1, target, prob/float(count));

            // most nodes will return 0, we only want the non-zero prob
            max_prob = max(max_prob, p);
        }

        return max_prob;
    }

    double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
        Graph g = buildGraph(edges);
        set<int> marked({1});

// start the search at the root node (1) with unit probability (1.0)
        return dfs(g, marked, 1, t, target, 1.0);
    }
};